Charges
Created Tuesday 24 May 2022
Let us begin. When I say begin, I mean little intro, so hold your breath.
You got charges, know the charge, be the charge, everything is charge, electric charge specifically. everyone has them, what is it? it took maxwell and a bunch of other dudes like a bunch of years to find out. its like. a property of matter, and is conserved. Remember these things, especially the conserved part, it will help you alot in integral calculations.
Electric charge can be thought of in terms of particles, these charged particles are divided by positive and negative charges. An electron, with it's antiparticle, the positron. REMEBER THAT, the electron is found on the standard model, with it's opposite, the positron, not the proton. The proton's opposite charge is an antiproton (go figure), not an electron.
This means though an electron has a negative charge, and the proton has a positive charge, that charge being equal and opposite to each other, they are not symmetric opposites.
However, it much better to think of charges as point charges, or single points. For the start, we will imagine they are just. Sitting there, doing nothing really. Chilling. They have their own quantized charge. Quantized, of course meaning a quantity of charged, which is conserved.
Remember kids, the total charge never changes if the system is isolated.
This means that the total electric charge of an isolated system, when you add them all up, does not change after anything.
1.0 Charge as a quantity
ok check it
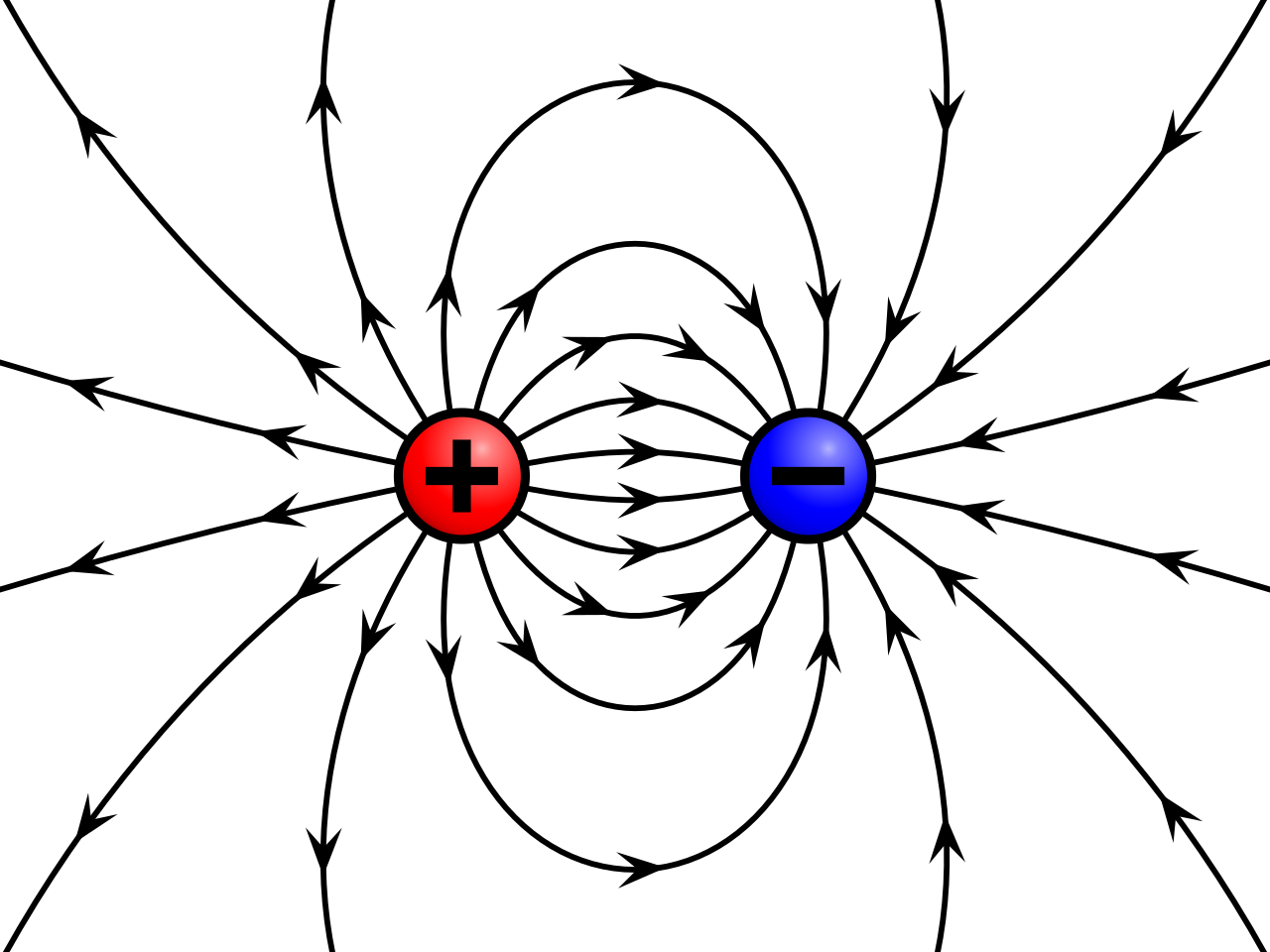
These are point charges. We can denote the magnitude of charge as e. Please note that as a physicist, you will know that hadrons, quarks, all have some partial charge, but let's be real for a second, the charge of one of these independent of nucleus or some other particle where it's charge can blosson, has not been identified, or so I'm told.
This doesn't really matter for our case, and we should get to the good stuff.
Just note that this is denoted as e, which is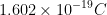 
What is C anyway? It's coloumb, the SI unit of charge. 1 Coloumb is what. Let's just word it like this:
Two like charges, each with 1 coloumb will repel each other with 8.988 * 10^9 Newtons. If they are one meter apart.
You may also think of it like, 1 Coloumb is the charge of 6.242 * 10^18 electrons.
Ok first equation write this down:
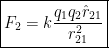
This is Coloumb's Law: the force between 2 charges.
Okay now what the fuck does this mean?
q1 and q2 are the scalars giving the magnitude and the sign of the charges. In Coloumbs. q1 is the first charge, and q2 is the second. Note that they can be negative, so account for that in the equation.
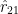is just the unit vector in the direction of charge 1 to charge 2.
F2 is just the charge acting on charge 2. Following this logic, if we wanted to find the force on charge 1:
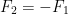
k is a constant. retrieved from the magnetic field we will talk about later. Just know its usually 8.988 * 10^9. 8.988 * 10^9 what? Apples? Bananas?
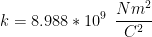
Are you happy? Actually this is important, look at the units. Now, I will use SI units because I think imperial units are cringe and that gauss, though a genius, was also a little loopy. It happens, all great men are a little loopy. That's why I'm a bit loopy. lol.
Why use imperial or Gaussian units in the first place though? For imperial units, you don't, that was never an option get out of here. But for Gaussian units it does make equations alot simpler for electrostatics and electrodynamics. Gauss made the unit of charge an electrostatic unit, or an esu, which is defined such that k is 1, no units. r21 is in cm, F is in dynes and q in esu.
Now that constant may look cool but actually you are not using it. You're actually going to be using this:
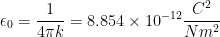
This means in terms of epsilon naught, the new equation needed is:
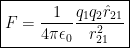
Either way you can see how it can be derived by the equation for the universal law of gravitation
1.1 More than 2 charges
Lets say we live in a universe. and that universe has more than just 2 charges. That sucks, oh wait measuring the force doesn't suck because of superposition.
This one took me a bit to wrap my head around so bear with me. I have an example to show how it works.
In high school math, you are brough up to believe that force is only useful in it's magnitude, except for that one section in math where they talk about vectors and it fucks you every time. In reality, if you want to be a physicist, you have to get used to the idea of vectors. You know what a vector is, and if you don't, I'll put in a page about it later. But for now, remeber vectors exist.
The formula for finding more than one charge is fairly simple to guess as a pattern and is as follows:
For any charge q3, the force acting on it by 2 other charges is:
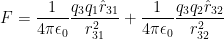
You can sort of see it really is just adding the two forces acting on q3. It sort of is, unlinke in gravitational bodies, where you have to account for the gravitational force of both objects, involves some gradients, etc. Important thing to note however is the vectors. They have an effect, and notice how the force is a vector sum.
Now take this problem here:
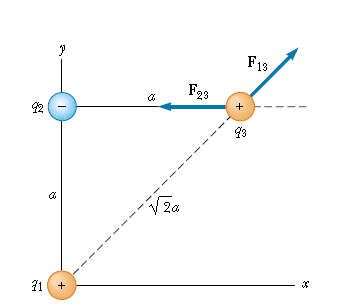
A 3 charge system, what is the force acting on q3?
Well you need a bit more information than that:
q1 = q3 = 5.0 μC
a = 0.1 m
q2 = -2.0 μC
Now you can answer what is the force acting on q3. Ok I will give you about 2 minutes to answer. Ready. Start.
Done. Okay Here's how to solve it.
First you must make the vectors of force, note that force vectors for q3 are sort of given to you. Because q2 is negative, it attracts q3. When I say vector, of course, I mean unit vector. Well, q32 vector is pretty easy, just a line pointing left on the x axis, unit vector of <-1, 0>. The unit vector for q1 to q3 however will be <cos 45, sin 45>, since it is pointing directly diagonal.
After this, plug all of these in to the equation above (and remember to convert μC to C), and you should get a vector answer, somewhere along the lines of <-1.1, 7.9>N. Of course, if you want total force, just take the magnitude of that. Total force is a weird phrase here. Resultant force? Idk.
1.2 Work
Millenial charges don't do any work, ruining our industries. Luckily, we work with charges that have been here since the conception of the universe (i bet that's older than you), and these charges can do work.
Essentially, the force equation I showed you is kinda it for electrostatics, that's sorta why youll never hear an ECE major study electrostatics. With coloumb's law we can also find the equillibrium arrangement as well. It's kind of like saying Newton's laws is all there is to motion. It's sorta true we just don't think it that way. We landed a rocket on the moon using the same equations derived by Newton. Why do we have rocket scientists then? Cause they do other stuff than predict the trajectory we got computers for that now.
So how does anything get done if we just look at Coloumb's law? easy, add work. Or energy, a better term. Why use energy? Because its real but also conservative (not politically but it is kind of old so maybe). It's from the phrase Conservation of energy, conserves itself, cant create, can't destroy. If you've taken calc 3 you know this makes every equation 100 times simpler, which is awesome.
Ok let's have two charges. And let's say, if we place them far apart, how much work do you need to bring em in close. Not for a hug, maybe a noticable distance. 5 feet apart. Because they're positive and negative charges so they're not gay. (is positive and negative charge gender??)
First let's think what work is.
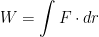
EZ, where dr is the displacement. Now most of the time in highschool math, you think of that as just multiplication, no integral, nothing. But we far from your highschool science class, get ready to derive:
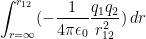
Crazy, I know, hold on, let me explain. The distance we imagined at the beginning was a bit further than a large distance. Actually it was an infinite distance, but if you were to graph this equation equation, you could see that at some point the force exerted on the two forces is so small that it's practically 0, we imagine to that point, until it's defined to a point where it actually matters. It goes all the way until the distance we want, which is r12. Anyway, it's kind of hard to work with that work equation, it's stuck in an integral. Hope you remember your integral rules, because this one should be self explanatory.
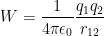
Great, now we have our work equation. As you know work is focused on displacement, meaning it really matters that we know the start and the end point. As such any path the charge takes is the same work (allowing us to believe the field is conservative) if these positions are the same.
This is hard to visualize, so here is an example.
This looks complicated at first but it can accurately explain the work e quation. q1 is fixed, q2 moved to the same position P from the same path. The first sphere is r, second is r + dr. The path must pass through both spheres. The work between each path is -F * ds in this bit of path, it also the same for every path. This is because F has the same magnitude at both places and directed radially from q1.
ds = dr/cos(theta), so F * ds = mag(F) dr. Remember F is a vector, so the force is the same, since the force is central.
Let's say we now had 2 charges like I explained before, only now there is a 3rd charge. 3 charges.
Gee, if only some loser who had too much free time even with a job somehow created a shitty ms paint drawing to visualize this!
I got you covered.
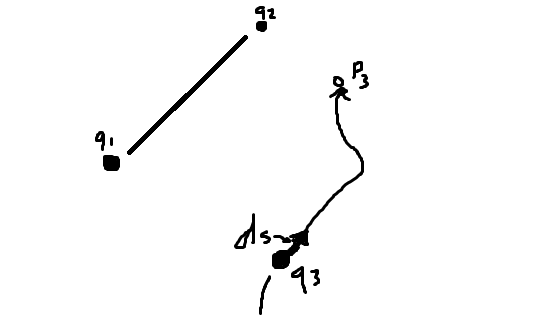
Check it. Okay I realize this really is shitty now that I've inserted it but whatever listen to the explanation youll get it.
q1 and q2 are distance r21 away. Get it. r21 because its r 2 to 1. q3 is also there, it came in from bum fuck nowhere which in science terms just means infinitely away. but now its moving to P_3, a point I have defined that exists. Let's say we wanted to know the work required to do this. EZ we did this like 10 milliseconds ago.
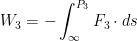
BQQM. Wait this is actually incomprehensible. Let's break it down a bit.
Why is it incomprehensible? Because we have never define F_3, and ds either. The integral itself is a line integral, we want to do a line integral because it is the amount of work done given by the electric field over a path. Check it:
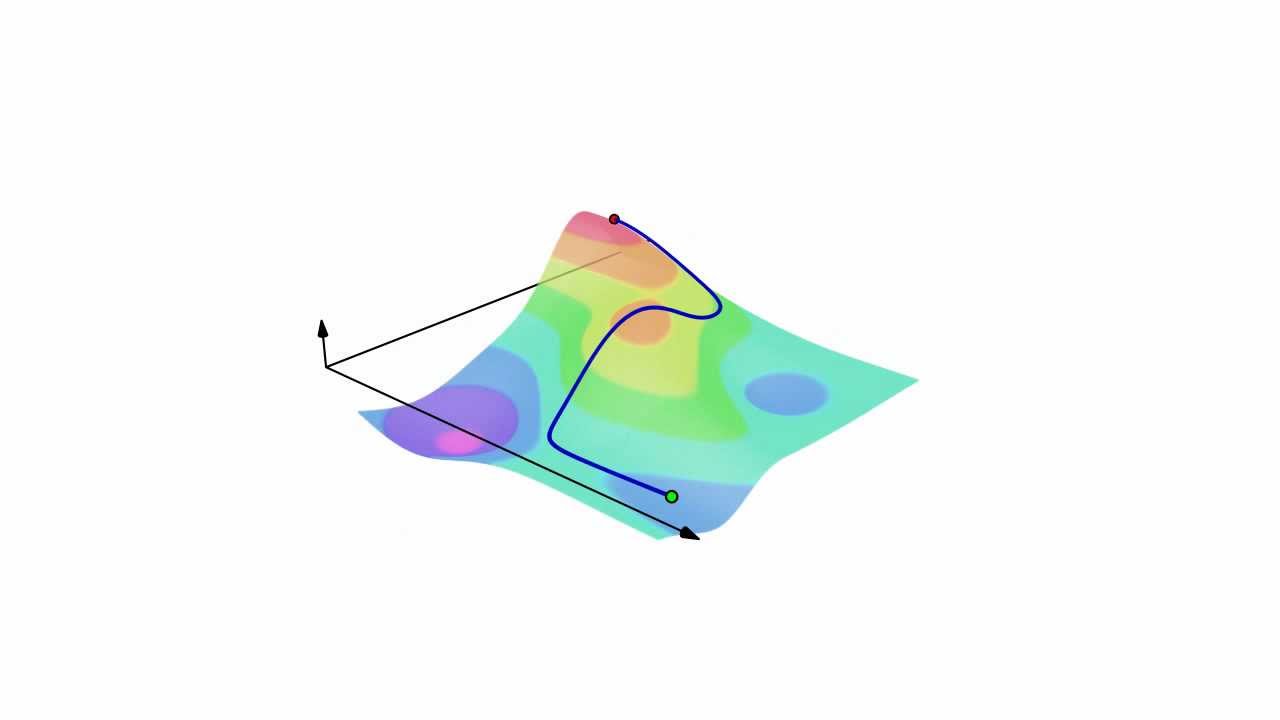
If you want a full explanation of a line integral, go online, but soon, there will be a calculus page.
Well, what can we define F_3 as? We know it is the additivity of the electrical interactions.
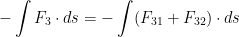
Great, hope you studied your integrals because now we can do a life hack with this, check it:
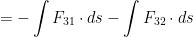
This means that this is just the work when q1 and q3 are alone, and q2 and q3 are alone, in order to bring q3 to P3.
Well, we also know those equations from above, allowing us to write this as:
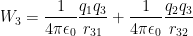
This allows us to say that the total work to assemble these charges, over the entire system (which we can denote as U) can be written as:
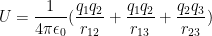
q3 was brought in last, depite this every charge appears symmetrically in the problem. Remember. Symmetry symmetry symmetry. Whenever its possibloe break it, otherwise, keep it.
Anyway, U can also be denoted as the electric potential energy of a system, so write that down. The truth is this is kinda arbitrary but dont worry about it. Just know in this case we just said 0 is any arrangement when the charges are infinetly far away, bum fuck away.
Also remember this electric potential energy belongs to the system as a whole. Remember that. No halfsies or thirdsies on this energy.
Now what we can secretly do with this is that we can apply this to any number of charges. So many, we can just call it N charges. You just have to sum over all the pairs. Heres the mathematical representation:
Double Sum Notation. Think of it as a nested for loop. You start at the first number for j, 1, and for k do every number up to N except for j. Wait, that counts every pair twice. We then put the 1/2 to correct it.
Why would we even need to know this? Easy, it's good to understand for crystal lattices. Like the salt u eat on your fries fatass
We know that the formula for salt is NaCl, and is a crystal lattice structure like this below:
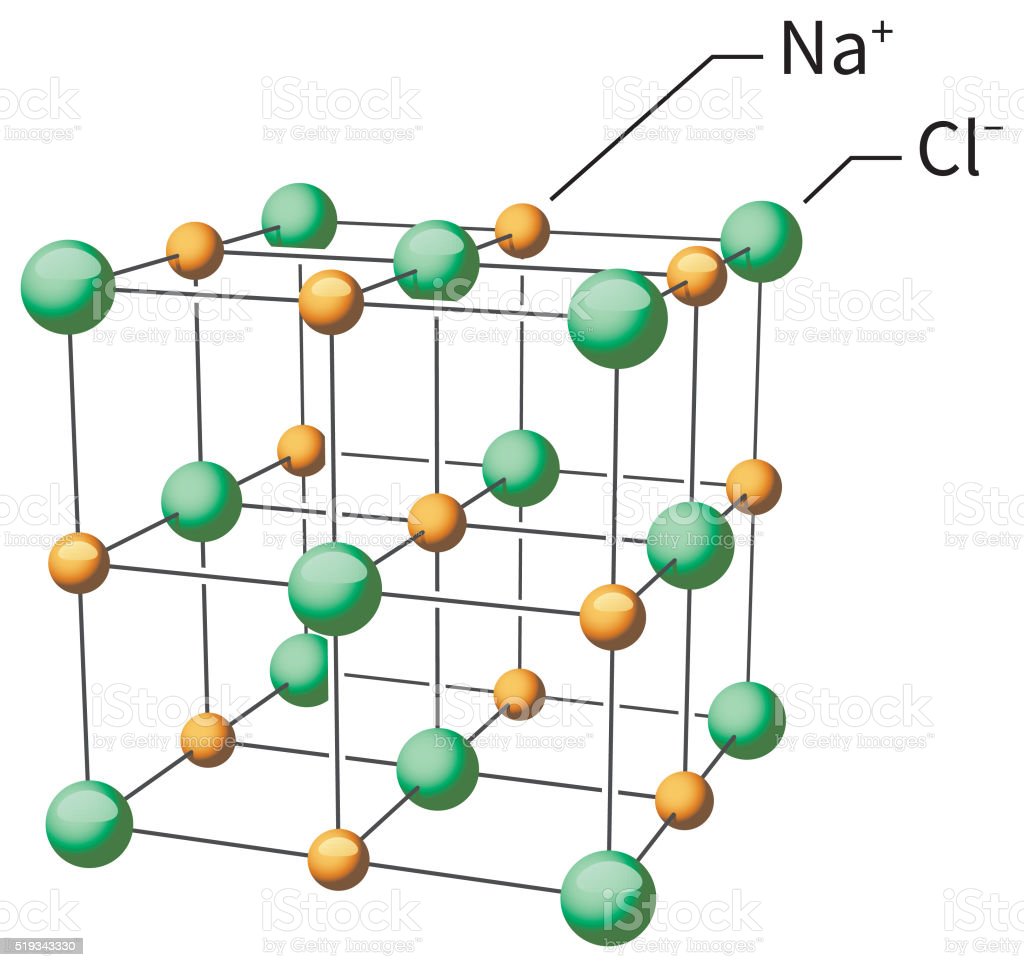
So beautiful. Anyway if you think about it, Na is a positive ion and Cl is a negative ion which is a close enough approximation to a charge. You can find the electric potential energy (the amount of work needed to be done to arrange this lattice) using the equation above using the distances of every ion in relation to each other. Easy. Only it's not easy because the average grain of salt has 10^20 atoms. Wait a second, sums can converge. Ok, let's see if that happens.
It is because of this 10^20 we see that putting together 2 grains of crystals takes a large amount of energy. You should calculate it for 1 gram per crystal. I assume you will need mathematica. That's beside the point.
This situation is confusing, luckily we have equal and opposite charges. Genius.
First thing you gotta realize is that this is a crystal. So that really means u can sorta work off the picture I gave above. Ok hard to explain but the arrangement of positive ions and negative ions is the same around each ion. It's weird. This however makes it an alternating sum. Why?
Well because instead of looking at every combination of every ion in the system, we can just look at one ion, and call it the center (you don't actually have to find the center ion but you should probably guesstimate somewhere close) and just loop over every diatnce for every atom to that one center, and then you can just multiply that by the number of atoms. I sound weird saying it in words, here's the equation:
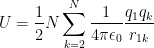
The leading terms then start as follows:
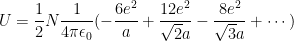
The first 3 terms are for the first 6 nearest chlorine ions at distance a.
As it turns out, the series does not absolutely converge, we would need to group them in shells in alternating sums rather than just adding all of the positive and negative ions. Even with your advanced math skills, this is just teadious and painful, so I will just give the answer, generated by mathematica.
